
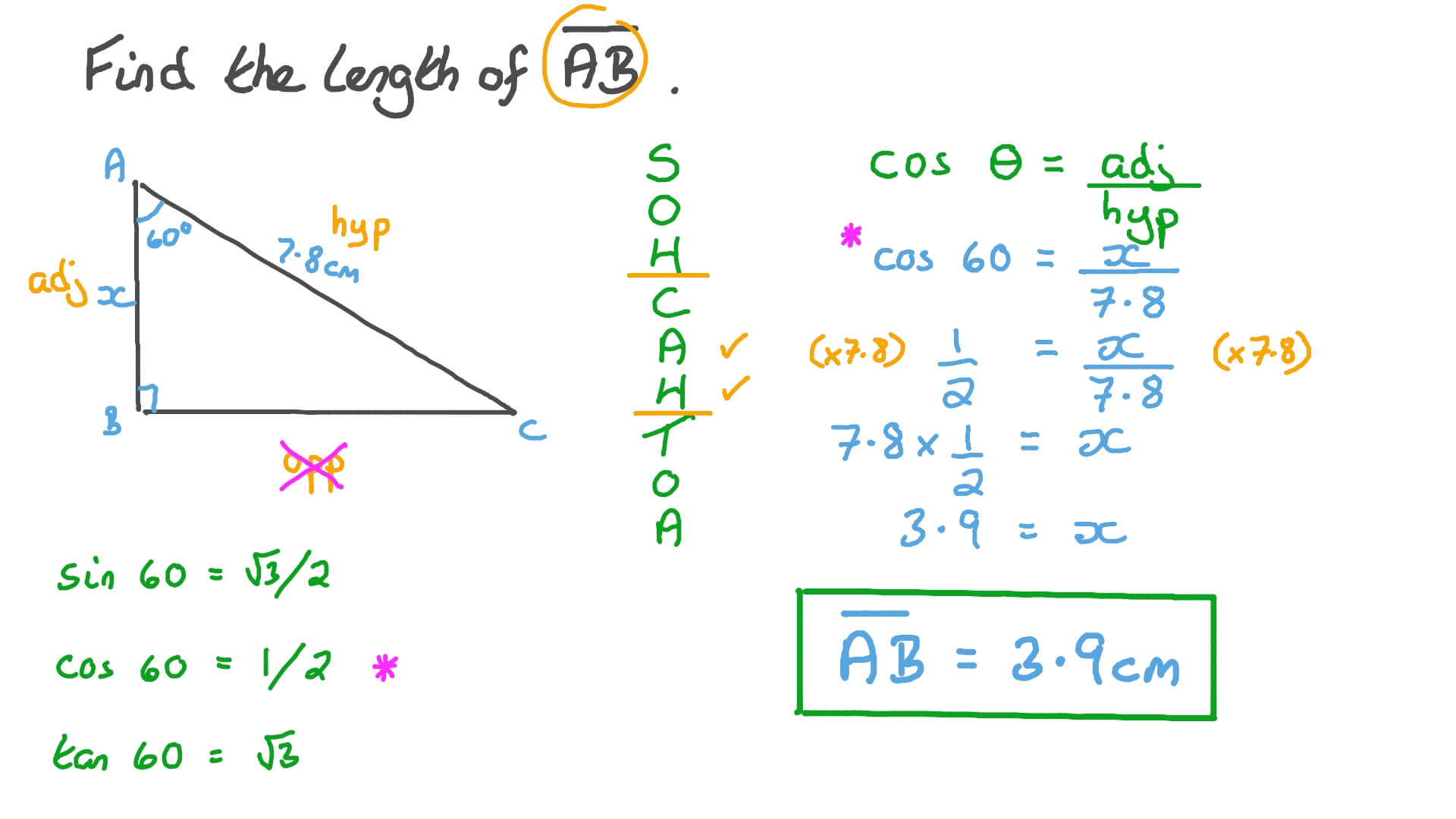
One approach students used in that followup conversation was the impossibility of many of the responses given the decimal approximations of the side lengths in radical form. But they made for great classroom conversation at the start of class the next day. They are signs of medium to massive misunderstanding. (2) Needless to say, the responses captured in these four images were more than mildly disappointing. So here’s my question: Did these students perform so terribly on this four-question exit slip because I was pushing them to be efficient before they were ready to be efficient? And if that’s the case, how do we know as teachers when our push for efficiency is actually detrimental for students? How do we know when an individual (or small group, or entire class) is ready to move from slow-and-steady-and-meaningful to generalized and more efficient? Should the push ever come from the teacher, or only from the student? Many students made meaningful observations/connections, some did not (as evidenced by the four images). They then looked for patterns among the 30º-60º-90º triangles, as well as the 45º-45º-90º triangles.

Therefore, we must first use our trigonometric ratios to find a second side length and then we can use the Pythagorean theorem to find our final missing side.(1) In the lesson leading up to this exit slip, the class used the Pythagorean theorem to find an unknown third side length (when given the first two).
#Rules for special right triangles how to
Q: How to use pythagorean theorem with only one side? A: If only one side length is known, we are unable to use the Pythagorean theorem. Q: How do you know if it’s a pythagorean triple? A: A right triangle whose side lengths are all positive integers, such as a 3:4:5 triangle or 5:12:13 triangle or 7:24:25 triangle. For example, 30:40:50 or 6:8:10 are both multiples of 3:4:5 and both indicate right triangle measurements. Additionally, all multiples are also right triangles. Consequently, if we are given these three side lengths we know it refers to a right triangle. In other words, 3:4:5 refers to a right triangle with side length of 3, 4, and 5, where the hypotenuse is the length of 5 and the legs are 3 and 4, respectively. Q: What is the 3:4:5 triangle rule? A: The 3-4-5 triangle rule uses this well known pythagorean triple. Then we will use the Pythagorean theorem to find the remaining side length. Q: How to do multi-step special right triangles? A: If we are given a right triangle with one acute angle and side length known, we will first utilize our special right triangle ratios to find one missing side length (either a leg or hypotenuse). We can find the hypotenuse by using the Pythagorean theorem or trigonometric ratios by fist ordering side lengths in increasing value, as seen in the video. Q: How to find the hypotenuse in special right triangles? A: The hypotenuse is always the longest side of a right triangle. Additionally, you will discover why it’s very important on how you choose your side lengths. In the video below, you will also explore the 30-60-90 triangle ratios and use them to solve triangles. Solve the right triangle for the missing side length and hypotenuse, using 45-45-90 special right triangle ratios. Consequently, knowing these ratios will help us to arrive at our answer quickly, but will also be vital in many circumstances. The Pythagorean theorem requires us to know two-side lengths therefore, we can’t always rely on it to solve a right triangle for missing sides. Rather than always having to rely on the Pythagorean theorem, we can use a particular ratio and save time with our calculations as Online Math Learning nicely states.Īdditionally, there are times when we are only given one side length, and we are asked to find the other two sides. Well, one of the greatest assets to knowing the special right triangle ratios is that it provides us with an alternative to our calculations when finding missing side lengths of a right triangle. Moreover, we will discover that no matter the size of our special right triangle, these ratios will always work.īut why do we need them if we have the Pythagorean theorem for finding side lengths of a right triangle? Together we will look at how easy it is to use these ratios to find missing side lengths, no matter if we are given a leg or hypotenuse.


 0 kommentar(er)
0 kommentar(er)
